In this assignment, we will investigate how a simple physical law may be modeled. We will discuss capacitors, and build a mthematical model based on a very basic physical relationship. We will examine some of the properties of this model, and examine spreadsheet applications for modeling.
In electronics, the capacitor is one of the most ubiquitous components. Capacitors store electrons, and are used in applications as diverse as power supply filtering (to reduce spikes in power), rectifying AC (which is sinosoidal) into DC (which is constant), timing circuits, and generating radio waves. A capacitor works by having two or more condensor plates upon which electrons can gather, but the plates are separated by a layer of non-conductive material, called a dielectric. Initially, the condensor plates will have the same number of electrons. When a capacitor is in-line with a voltage source (battery or otherwise), one plate fills with electrons, while the other is voided of the same number. You can think of each electron added to one plate having the charge needed to displace an electron from the other plate. Since like charges repel, the electrons added to one plate by the force of the battery force the electrons from the opposite plate.
One of the most useful properties of the capacitor, which we'll explore, is its charge and discharge time. This property is utilized in very diverse applications: flashing lights, timers, counters, etc. Studying the very simple physics principles involved can teach us a lot about functions and offers some insight into how math and physics overlap.
To begin with, we state what is called Coulomb's Law, which predicts the amount of force between two electrons: F = k*q1q2/r2. k is a constant, which we're not going to derive. q1 and q2 are the charges on two points. For our electrons, the charges are -1. Our force, then, is always going to be positive, corresponding to a repulsive force. Finally, r is the distance between the two charges.
Let's take a detailed look at how this force changes as we charge the capacitor. Since this force involves a constant k, we can ignore it and focus on the relative force between the electrons. We're going to assume that the condenser plates are narrow enough to only allow the electrons to lie in a line of length L, which means we only have to worry about the linear separation between electrons. Since they all have an equal, repulsive, charge, they will maximize the space between them, and therefore r = L/(n-1), where n is the number of electrons in the capacitor. We'll scale this so that L = 1.
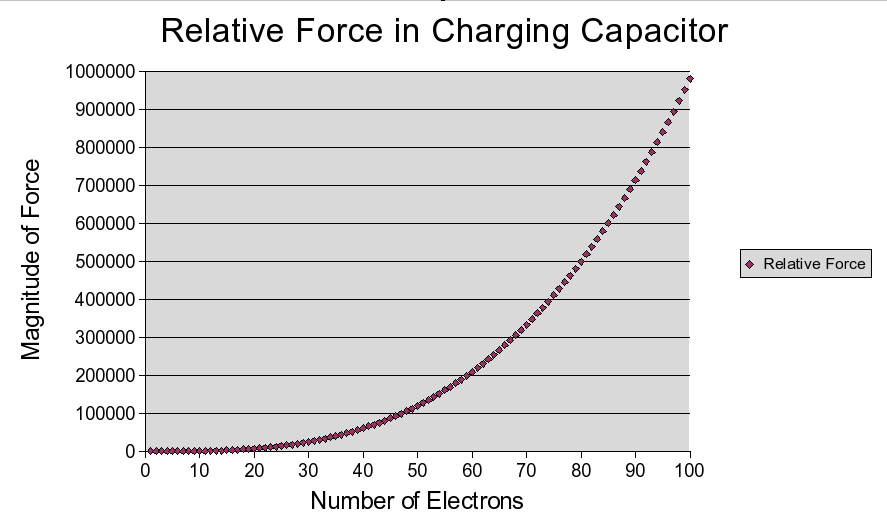
We connect the voltage supply, and charge the capacitor. We'll assume our capacitor holds exactly 100 electrons when it is fully charged. Our first electron in the capacitor experiences no force on it, and contributes 1 eV of charge (eV is short for electron volt, the measure of charge on one electron) to the capacitor. Our second electron contributes 1 eV of charge, and a relative force of 2 (2eV/12). Our third electron contributes another 1 eV of charge, but now we have a relative force of 12: 3eV*22. We can then write a formula for the total relative force in the capacitor as electrons are added. Let n be the electron we are adding. Then there is a total charge of n, and a separation of r = 1/(n-1), so our force is f(n) = n*(n-1)2.
We can chart this on a spreadsheet to analyze this behavior.

WHOA!! The electrons in the capacitor experience almost 500,000 times the force with the addition of the 100th electron than with the 2nd . Notice also that from the 2nd to the 50th, there is a difference of 10,000, but from the 50th to the 100th, the difference is over 900,000!
Still, we haven't covered any new ground, mathematically speaking. We did develop a mathematical model from a physical relationship, but our function is only a dramatic case of a third degree polynomial. Let's ask another question, one that will expose us to something new.
Suppose we charge our capacitor fully, so that it has 100 electrons. In this state, it has enough force to expel 10 electrons in the first second. How does the discharge of electrons then proceed?
After the first second, we have lost 10% of our total charge, leaving 90 eV. Our separation has gone from 1/99 to 1/89, so 1/r2 has gone from 9801 to 7921, and so our force has gone from 9801*100 to 7921*90, from 980100 to 712890, for a decrease to about 72% of the original force. In the third second, we have enough force to kick out 7 more electrons. Then we have 83 eV remaining. We have r2 = 822 = 6724, for a force of 558092 remaining, about 57% of the original. In the fourth second, we expel 6, leaving 77, for a force of 444752, 45%.
Once again, we'll turn to a spreadsheet to help us visualize this process over time, but I will make one change, which is to start with 1000 electrons. The reasoning is still the same... we'll start with 10 electrons lost in our first second and proceed from there, but we'll have more numbers to see a pattern emerge:
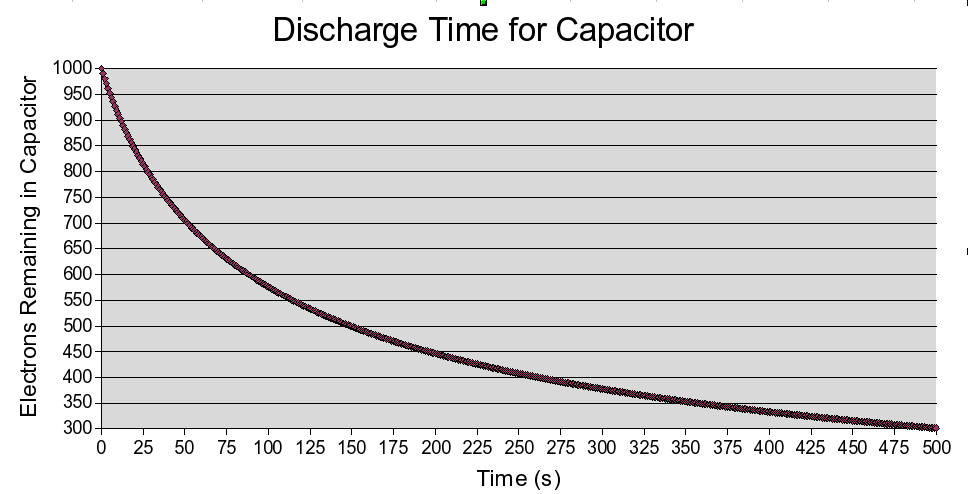
500 seconds, and the capacitor still has 300 or so electrons left in it! What's more, the function appears to be slowing down more and more as time progresses. This does not seem to be one of our familiar polynomial functions, and it certainly isn't a cyclic trig function. This represents the third category of function mentioned in lesson one, the exponential. Our particular case is one of exponential decay.
The key to recognizing an exponential function is the following:
We have a situation in which we are told an initial rate of change for the situation. In the capacitor, our initial rate of change was the 10 electrons in 1 second. However, the change in the function (the loss of 10 electrons) affects the rate of change. In our case, the loss of 10 electrons not only reduced the charge by 10 (a linear change), but also increased the distance between the electrons (a quadratic change). This change in the value of the function directly affects the rate of change for the next batch of electrons to leave, in a repeating process, and you can now visualize a feedback loop. If the change in the value of the function increases rate of change in the function, the loop is re-inforcing, and the function is one of exponential growth. If the value of the function decreases the rate of change, we have a negative feedback loop, and the function is one of exponential decay.
Exponential functions are characterized by the value of the function affecting the rate of change of the function. As a class of function, they are ubiquitous in nature and society: population growth, radioactive decay, compounded interest in finance, gravity tugging on a hanging chain, and many others, including our capacitor discharging. Anytime the result of a function contributes to its rate of change, an exponential function involved.
What about charging our capacitor? We'll start with two electrons in the capacitor for a force of 2, then reverse our discharge process, allowing 10 electrons into the capacitor in the first second. So now we have 12 eV and r2 = 1/121, for a force of 12*121 = 1452. The next ten electrons will increase the charge to 22 eV and the force to 22*212 = 9702. The difference, 8252, is 85% of the total, so this batch of ten electrons took about 1.17s to enter the capacitor. If you guessed it's time for a spread sheet... fresh and hot:
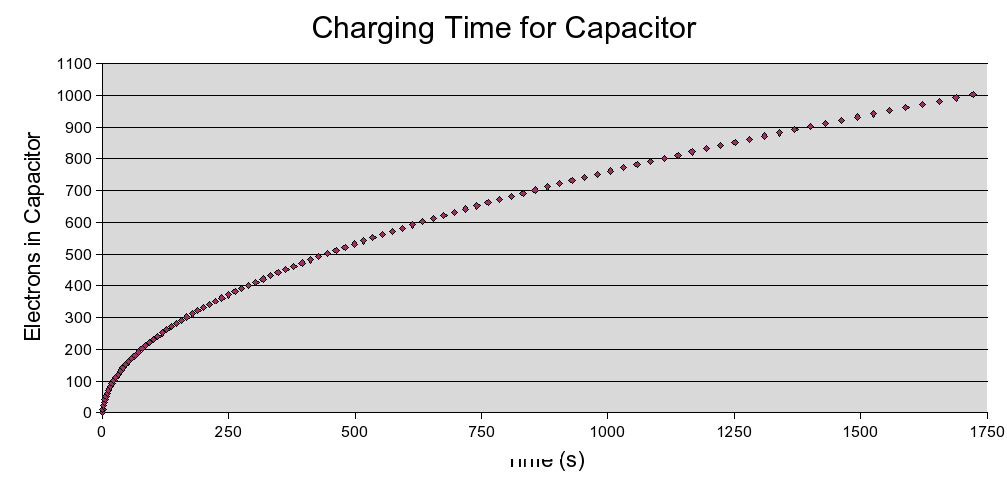
What we have now is the inverse function for an exponential function, known as a logarithmic function. If you look back at how we reasoned in setting up the functions and contrast our processes for the charge and discharge cycles, you'll notice that in the discharge (exponential decay), we were interested in the cumulative loss of charge (which we actually looked at as the charge remaining) compared to the initial, while in the charge cycle (logarithmic growth), we looked at each subsequent difference in charge. The quite subtle reason for this difference, and the key to understanding the relationship between the two, is that in the discharge, we were analyzing the rate of change of the number of electrons per second. In other words, we were always asking how many elctrons will exit in 1 second (electrons/sec). In the charging analysis, we were asking how many seconds were need for a fixed number (10) of electrons (sec/electrons). In a physical sense, we were examining inverse situations (charge vs. discharge), charting their respective rates of change (sec/electrons vs electrons/sec), and in the process detailed two inverse functions, exponential decay vs. logarithmic growth.